线段树（懒标记）总结

例题

题目描述
输入输出格式
输入输出样例
说明

线段树的定义和构造
区间更新与懒标记

懒标记
如何进行区间更新

区间查询
完整代码（注释版）
参考

线段树是非常基础的算法了……

线段树是一种二叉树，可视为树状数组的变种，最早出现在2001年，由程序竞赛选手发明。我们ZS老师说过：“所有可以用树状数组解决的题目都可以用线段树解决，但是部分线段数可以解决的题目却无法用树状数组解决。”由此可见线段树十分强大……

此资料结构实际应用用途不大，但由于其程式易于实作而被广泛应用于程式竞赛当中。其用途是在$O(\log N)$查询一个指定区间内的资讯，并可在同样的时间复杂度支援更新等操作。
——维基百科

例题

先来看看洛谷上的线段树模版题：【模板】线段树 1

题目描述

如题，已知一个数列，你需要进行下面两种操作：
1.将某区间每一个数加上x
2.求出某区间每一个数的和

输入输出格式

输入格式：
第一行包含两个整数N、M，分别表示该数列数字的个数和操作的总个数。
第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。
接下来M行每行包含3或4个整数，表示一个操作，具体如下：
操作1：格式：1 x y k 含义：将区间[x,y]内每个数加上k
操作2：格式：2 x y 含义：输出区间[x,y]内每个数的和

输出格式：
输出包含若干行整数，即为所有操作2的结果。

输入输出样例

输入样例

输出样例

11
8
20

说明

时空限制：1000ms,128M
数据规模：
对于30%的数据：N<=8，M<=10
对于70%的数据：N<=1000，M<=10000
对于100%的数据：N<=100000，M<=100000
（数据已经过加强^_^，保证在int64/long long数据范围内）
样例说明：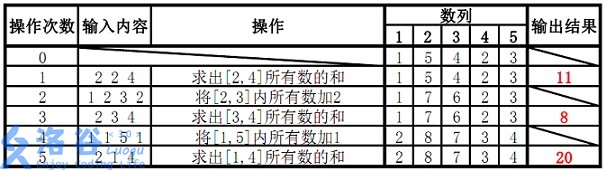
title=

线段树的定义和构造

线段树（Segment Tree）是一个平衡的二叉树，所有叶子到根的距离最多只差1。令整个区间的长度为N，则其有N个叶节点，每个叶节点代表一个单位区间，每个内部结点代表的区间为其两个儿子代表区间的联集。

翻译成人话就是：线段树是个二叉树，每个节点表示一个区间（或许应该叫区间树……），叶节点代表的区间大小是1（即单位区间）。（以上面的例题为例）很容易理解，根据叶节点我们可以向上累计，对于每个非叶节点，很容易构造出其代表的区间内所有数字加和（以下称为“管辖区间和”（我自己起的名字……因为我觉得“管辖”这个词很高端……），用tree[x]表示x节点管辖区间和）（即每个点左右儿子代表区间和的加和）。这样向上构造，我们就可以造出一颗线段树。这就是build函数构造线段树的过程：

inline void build(int p,int tl,int tr){
    tag[p]=0;
    if (tl==tr) {tree[p]=a[tl];return;}
    int mid=((tr-tl)>>1)+tl;
    build((p<<1)  ,tl,mid  );
    build((p<<1)+1,mid+1,tr);
    tree[p]=tree[p<<1]+tree[(p<<1)+1];
}

区间更新与懒标记

如果没有区间更新，我们就用不到懒标记了，因为对于单点更新，直接向上推，$O(\log_2 N)$的时间内就可以得出结果。但是区间更新就十分麻烦：如果一个个单点进行更新，最高需要$O(N* \log_2 N)$！显然很容易超时。懒标记（Lazy Tag）其实是对朴素的线段树的一个优化，可以让区间更新也达到$O(\log_2 N)$级别。所以首先我们来认识一下懒标记：

懒标记

懒标记（Lazy Tag），也有的地方翻译成“延迟标记”（听起来高端……），就是指在更新一部分区间的时候，不更新这个区间里面的每个点，而是（懒惰地）把这个区间分割成很多个能用线段树上的点表示的区间（当然是分的区间越少越好，也就是说每个区间越大越好），只修正代表这个区间的点，再把这些区间标记下，下次如果要查询的区间与这个区间有交集并且没有包含这个区间，就说明需要“分割”这个区间，再将这个区间向下修正。这样时间复杂度就可以优化很多。

如何进行区间更新

刚才已经提到，如果要把区间[L,R]中所有元素加上delta，则只需要从线段树的根节点开始向下寻找，找到第一个被[L,R]包含的区间，就修正这个区间（注意“修正这个区间”只是增加这个区间和的标记和懒标记，不是把这个区间向下修正），然后继续向下找，直到找出来的一段段区间把[L,R]都覆盖了。

区间查询

区间查询和区间更新有点类似，假设要查询[L,R]，同样从根节点开始乡向下“分割”，不同之处在于：可能需要将刚才的懒标记用于向下修正。（具体见代码～）

完整代码（注释版）

#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
const int maxn=2000005;
int n,m;
long long a[maxn],tree[maxn],tag[maxn];
inline int read(){
    int ret=0,f=1;char ch=getchar();
    while (ch<'0'||ch>'9') {if (ch=='-') f=-1;ch=getchar();}
    while (ch>='0'&&ch<='9') ret=ret*10+ch-'0',ch=getchar();
    return ret*f;
}
inline long long llread(){
    long long ret=0,f=1;char ch=getchar();
    while (ch<'0'||ch>'9') {if (ch=='-') f=(long long)-1;ch=getchar();}
    while (ch>='0'&&ch<='9') ret=ret*(long long)10+(long long)(ch-'0'),ch=getchar();
    return (long long)ret*f;
}
inline void build(int p,int tl,int tr){  //构造Segment Tree 
    tag[p]=0;
    if (tl==tr) {tree[p]=a[tl];return;}
    int mid=((tr-tl)>>1)+tl;
    build((p<<1)  ,tl,mid  );
    build((p<<1)+1,mid+1,tr);
    tree[p]=tree[p<<1]+tree[(p<<1)+1];
}
inline void push_down(int tl,int tr,int p){  //push_down函数负责向下传递，将存储的tag数组用于修正 
    int mid=((tr-tl)>>1)+tl;
    tree[p<<1]+=(long long)tag[p]*(mid-tl+1);  //只需要修正一对左右儿子，不需要一直传递到叶节点 
    tag[p<<1]+=tag[p];  //因为没有往下修正，所以要把儿子的tag累计上 
    tree[(p<<1)+1]+=(long long)tag[p]*(tr-mid);
    tag[(p<<1)+1]+=tag[p];
    tag[p]=0;
}
inline void update(int sl,int sr,int tl,int tr,long long delta,int p){
    if (sl<=tl&&sr>=tr){  //p管辖的区间在修改范围内 
        tree[p]+=delta*(long long)(tr-tl+1);
        tag[p]+=delta;  //tag数组记录剩下的未向下传递的，实现“lazy tag”
        return;
    }
    push_down(tl,tr,p);  //如果没有完全包含p管辖的区间，则说明应该向下“分割”，所以应该用tag数组先修正下面的tree[] 
    int mid=((tr-tl)>>1)+tl;  //分割[tl,tr]区间 
    if (sl<=mid) update(sl,sr,tl,mid,delta,p<<1);
    if (mid<sr)  update(sl,sr,mid+1,tr,delta,(p<<1)+1);
    tree[p]=tree[p<<1]+tree[(p<<1)+1];  //向上累计 
}
inline long long query(int sl,int sr,int tl,int tr,int p){  //查询操作 
    if (sl<=tl&&sr>=tr) return tree[p];  //如果完全包含p所管辖的区间则直接返回tree[p] 
    long long ret=0;  //否则就“分割” 
    push_down(tl,tr,p);  //先要把当前的tag用于修正下面两个儿子，这样才能保证下面query用到的tree[]是正确的 
    int mid=((tr-tl)>>1)+tl;
    if (sl<=mid) ret+=(long long)query(sl,sr,tl,mid,p<<1);
    if (mid<sr)  ret+=(long long)query(sl,sr,mid+1,tr,(p<<1)+1);
    return ret;
}
int main(){
    freopen("tree.in","r",stdin);
    freopen("tree.out","w",stdout);
    n=read();m=read();
    for (int i=1;i<=n;i++) a[i]=llread();
    build(1,1,n);
    for (int i=1;i<=m;i++){
        int c=read();
        if (c==1){
            int x=read(),y=read();
            long long z=llread();
            update(x,y,1,n,z,1);
        } else
        if (c==2){
            int x=read(),y=read();
            printf("%lld\n",query(x,y,1,n,1));
        }
    }
    return 0;
}

参考

https://www.luogu.org/blog/pks-LOVING/senior-data-structure-qian-tan-xian-duan-shu-segment-tree
https://baike.baidu.com/item/%E7%BA%BF%E6%AE%B5%E6%A0%91/10983506
https://zh.wikipedia.org/zh/%E7%B7%9A%E6%AE%B5%E6%A8%B9_(%E5%84%B2%E5%AD%98%E5%8D%80%E9%96%93) "https://zh.wikipedia.org/zh/%E7%B7%9A%E6%AE%B5%E6%A8%B9_(%E5%84%B2%E5%AD%98%E5%8D%80%E9%96%93)")

SkyWT

我们的征途是星辰大海