Description
Ivan wants to make a necklace as a present to his beloved girl. A necklace is a cyclic sequence of beads of different colors. Ivan says that necklace is beautiful relative to the cut point between two adjacent beads, if the chain of beads remaining after this cut is a palindrome (reads the same forward and backward).
Ivan has beads of n colors. He wants to make a necklace, such that it's beautiful relative to as many cuts as possible. He certainly wants to use all the beads. Help him to make the most beautiful necklace.
- time limit per test: 2 seconds
- memory limit per test: 256 megabytes
- input: standard input
- output: standard output
Input
The first line of the input contains a single number $n (1 ≤ n ≤ 26)$ — the number of colors of beads. The second line contains after n positive integers $a_i$ — the quantity of beads of $i$-th color. It is guaranteed that the sum of $a_i$ is at least 2 and does not exceed 100 000.
Output
In the first line print a single number — the maximum number of beautiful cuts that a necklace composed from given beads may have. In the second line print any example of such necklace.
Each color of the beads should be represented by the corresponding lowercase English letter (starting with a). As the necklace is cyclic, print it starting from any point.
Examples
Input #1
3
4 2 1
Output #1
1
abacaba
Input #2
1
4
Output #2
4
aaaa
Input #3
2
1 1
Output #3
0
ab
Note
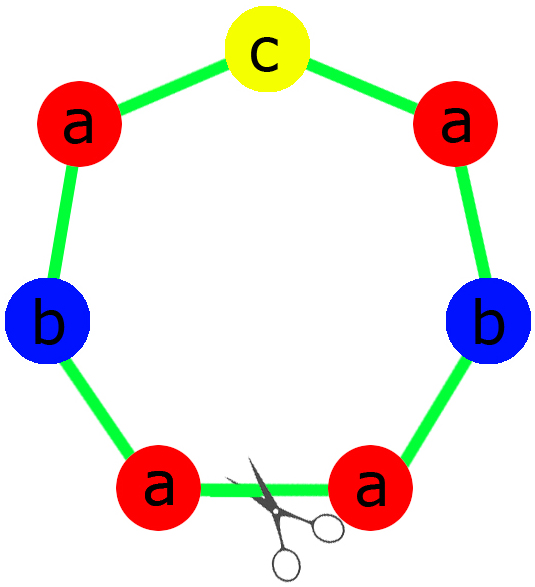
In the first sample a necklace can have at most one beautiful cut. The example of such a necklace is shown on the picture.
In the second sample there is only one way to compose a necklace.
Translation
题意:给你 n 种字符,请你确定一个排列顺序,把它们排成一个环。如果在这个环上某位置切一刀形成的一个字符串是回文串,则说这个切割是 beautiful cut,现在需要你排成的环能切出最多的 beautiful cut,并且要求输出这个环。
Analysis
直接考虑最后形成的一个环,如果我们在 a 位置切一刀可以形成一个回文串,在 b 位置也可以,那么在 a 关于 b 对称的位置也一定可以,在 b 关于 a 对称的位置也一定可以……这样整个环会被分为几等分。不难发现,每一份的长度就是所有种类字符数量的 gcd。
接下来需要考虑每段如何构造。为了关于切割点对称,每段必须呈 abc-cba-abc-cba-... 排列,最后回到 abc。
但是!如果有奇数段,最后就不能回到 abc(最后到 abc 位置轮到的是 cba)。这时候就要求每一段也是回文串,这样才能保证 abc 和 cba 相同。
不难发现,只允许有一个 $a_i$ 为奇数,如果有两个就为 0 了。分有无奇数考虑:
- 有一个奇数:每段都是回文的,这个奇数的字母必然放在每段中间;
- 全偶数:每段任意,只要关于切割点对称即可。
Code
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<vector>
#include<queue>
using namespace std;
#define int long long
inline int read(){
int ret=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9') {if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9') ret=ret*10+ch-'0',ch=getchar();
return ret*f;
}
const int maxn=30;
int n;
int a[maxn];
inline void imp(){
printf("0\n");
for (int i=1;i<=n;i++){
for (int j=1;j<=a[i];j++) putchar(i+'a'-1);
}
printf("\n");
}
inline int gcd(int x,int y){
return y?gcd(y,x%y):x;
}
signed main(){
n=read();bool flg=false,no=false;
for (int i=1;i<=n;i++){
a[i]=read();
if ((a[i]&1) && flg) no=true;
if (a[i]&1) flg=true;
}
if (no){
imp();
return 0;
}
if (n==1){
printf("%lld\n",a[1]);
for (int i=1;i<=a[1];i++) putchar('a');
printf("\n");
return 0;
}
int g;
g=a[1];
for (int i=2;i<=n;i++) g=gcd(g,a[i]);
if (!flg){
printf("%lld\n",g);
string otp1="",opt2="";
for (int i=1;i<=n;i++){
for (int j=1;j<=a[i]/g;j++) otp1+=(char)(i+'a'-1);
}
for (int i=n;i>=1;i--){
for (int j=1;j<=a[i]/g;j++) opt2+=(char)(i+'a'-1);
}
for (int i=1;i<=g;i++) if (i&1) cout<<otp1; else cout<<opt2;
printf("\n");
} else {
printf("%lld\n",g);
string opt="";int mid;
for (int i=1;i<=n;i++) if (a[i]&1) {mid=i;break;}
for (int i=1;i<=n;i++) if (i!=mid){
for (int j=1;j<=a[i]/g/2;j++) opt+=(char)(i+'a'-1);
}
for (int i=1;i<=a[mid]/g;i++) opt+=(char)(mid+'a'-1);
for (int i=n;i>=1;i--) if (i!=mid){
for (int j=1;j<=a[i]/g/2;j++) opt+=(char)(i+'a'-1);
}
for (int i=1;i<=g;i++) cout<<opt;
printf("\n");
}
return 0;
}
February 1st, 2019 at 07:54 pm
这就是。。。差距吗